从泰勒展开推导弹性波动方程的有限差分近似

Tintingo / 2022-02-22

Categories: WaveEquation / Tags: WaveEquation, FDM / Word Count: 1286

以一维弹性波动方程为例：

$\begin{matrix} (1) & \frac{\partial^{2} u (x, t)}{\partial x^{2}} = \frac{1}{c^{2}} \frac{\partial^{2} u (x, t)}{\partial t^{2}} + f (x, t) \end{matrix}$

式中，位移 $u (x, t)$ 是空间坐标 x 和时间 t 的单值连续函数， $c$ 为波速， $f (x, t)$ 为源项。

从泰勒展开推导弹性波动方程的有限差分近似

空间差分算子的推导

首先对位移函数 $u (x, t)$ 在坐标 $x$ 两侧附近作泰勒展开：

$\begin{matrix} (2) & u (x + Δ x, t) = u (x, t) + Δ x \frac{\partial u (x, t)}{\partial x} + \frac{1}{2} Δ x^{2} \frac{\partial^{2} u (x, t)}{\partial x^{2}} + \frac{1}{6} Δ x^{3} \frac{\partial^{3} u (x, t)}{\partial x^{3}} + \dots \end{matrix}$

$\begin{matrix} (3) & u (x - Δ x, t) = u (x, t) - Δ x \frac{\partial u (x, t)}{\partial x} + \frac{1}{2} Δ x^{2} \frac{\partial^{2} u (x, t)}{\partial x^{2}} - \frac{1}{6} Δ x^{3} \frac{\partial^{3} u (x, t)}{\partial x^{3}} + \dots \end{matrix}$

位移对空间一阶偏导数的近似形式推导

用式 $2$ 减去式 $3$ ：

$u (x + Δ x, t) - u (x - Δ x, t) = 2 Δ \frac{\partial u (x, t)}{\partial x} + \frac{1}{3} Δ x^{3} \frac{\partial^{3} u (x, t)}{\partial x^{3}} + O (Δ x^{4})$

将 $\frac{\partial u (x, t)}{\partial x}$ 移到左边，就可以得到：

$\frac{\partial u (x, t)}{\partial x} = \frac{u (x + Δ x, t) - u (x - Δ x, t)}{2 Δ x} - \frac{1}{6} Δ x^{2} \frac{\partial^{3} u (x, t)}{\partial x^{3}} - O (Δ x^{3})$

考虑到 $Δ x \to 0$ 是一个小量，因此得到：

$\frac{\partial u (x, t)}{\partial x} = \frac{u (x + Δ x, t) - u (x - Δ x, t)}{2 Δ x} + O (Δ x^{2}) = D_{x} u + O (Δ x^{2})$

式中， $D_{x}$ 称为 差分算子 ， $O (Δ x^{2})$ 称为差分算子的 截断误差 。

与公式中的其他项相比，小量 $Δ x$ 的二阶及更高阶指数项可以忽略时，得到 位移对空间一阶偏导数的近似形式 ：

$\begin{matrix} (4) & \frac{\partial u (x, t)}{\partial x} \approx D_{x} u = \frac{u (x + Δ x, t) - u (x - Δ x, t)}{2 Δ x} \end{matrix}$

位移对空间二阶偏导数的近似形式推导

用式 $2$ 加上式 $3$ ，得到：

$u (x + Δ x, t) + u (x - Δ x, t) = 2 u (x, t) + Δ x^{2} \frac{\partial^{2} u (x, t)}{\partial x^{2}} + O (Δ x^{4})$

将 $\frac{\partial^{2} u (x, t)}{\partial x^{2}}$ 移到左边，整理为：

$\frac{\partial^{2} u (x, t)}{\partial x^{2}} = \frac{u (x + Δ x, t) + u (x - Δ x, t) - 2 u (x, t)}{Δ x^{2}} + O (Δ x^{2}) = D_{x x} u + O (Δ x^{2})$

式中， $D_{x x}$ 为 二阶差分算子 ， $O (Δ x^{2})$ 称为差分算子的 截断误差 。

与公式中的其他项相比，小量 $Δ x$ 的二阶及更高阶指数项可以忽略时，得到 位移对空间二阶偏导数的近似形式 ：

$\begin{matrix} (5) & \frac{\partial^{2} u (x, t)}{\partial x^{2}} \approx D_{x x} u = \frac{u (x + Δ x, t) + u (x - Δ x, t) - 2 u (x, t)}{Δ x^{2}} \end{matrix}$

因此，位移函数在坐标 x 处的一阶和二阶偏导数，都可以近似表示为 x 附近函数值的差商形式，截断误差均为 $O (Δ x^{2})$ 。

时间差分算子的推导

首先对位移函数 $u (x, t)$ 在坐标 $t$ 两侧附近作泰勒展开：

$\begin{matrix} (6) & u (x, t + Δ t) = u (x, t) + Δ t \frac{\partial u (x, t)}{\partial t} + \frac{1}{2} Δ t^{2} \frac{\partial^{2} u (x, t)}{\partial t^{2}} + \frac{1}{6} Δ t^{3} \frac{\partial^{3} u (x, t)}{\partial t^{3}} + \dots \end{matrix}$

$\begin{matrix} (7) & u (x, t - Δ t) = u (x, t) - Δ t \frac{\partial u (x, t)}{\partial t} + \frac{1}{2} Δ t^{2} \frac{\partial^{2} u (x, t)}{\partial t^{2}} - \frac{1}{6} Δ t^{3} \frac{\partial^{3} u (x, t)}{\partial t^{3}} + \dots \end{matrix}$

与上述空间差分算子的推导过程类似，位移函数对时间的偏导数用差分算子 $D_{t}$ , $D_{t t}$ 表示为：

$\begin{matrix} (8) & \frac{\partial u (x, t)}{\partial t} \approx D_{t} u = \frac{u (x, t + Δ t) - u (x, t + Δ t)}{2 Δ t} \end{matrix}$

$\begin{matrix} (9) & \frac{\partial^{2} u (x, t)}{\partial t^{2}} \approx D_{t t} u = \frac{u (x, t + Δ t) + u (x, t + Δ t) - 2 u (x, t)}{Δ t^{2}} \end{matrix}$

截断误差为 $O (Δ t^{2})$ 。

一维波动方程的有限差分近似

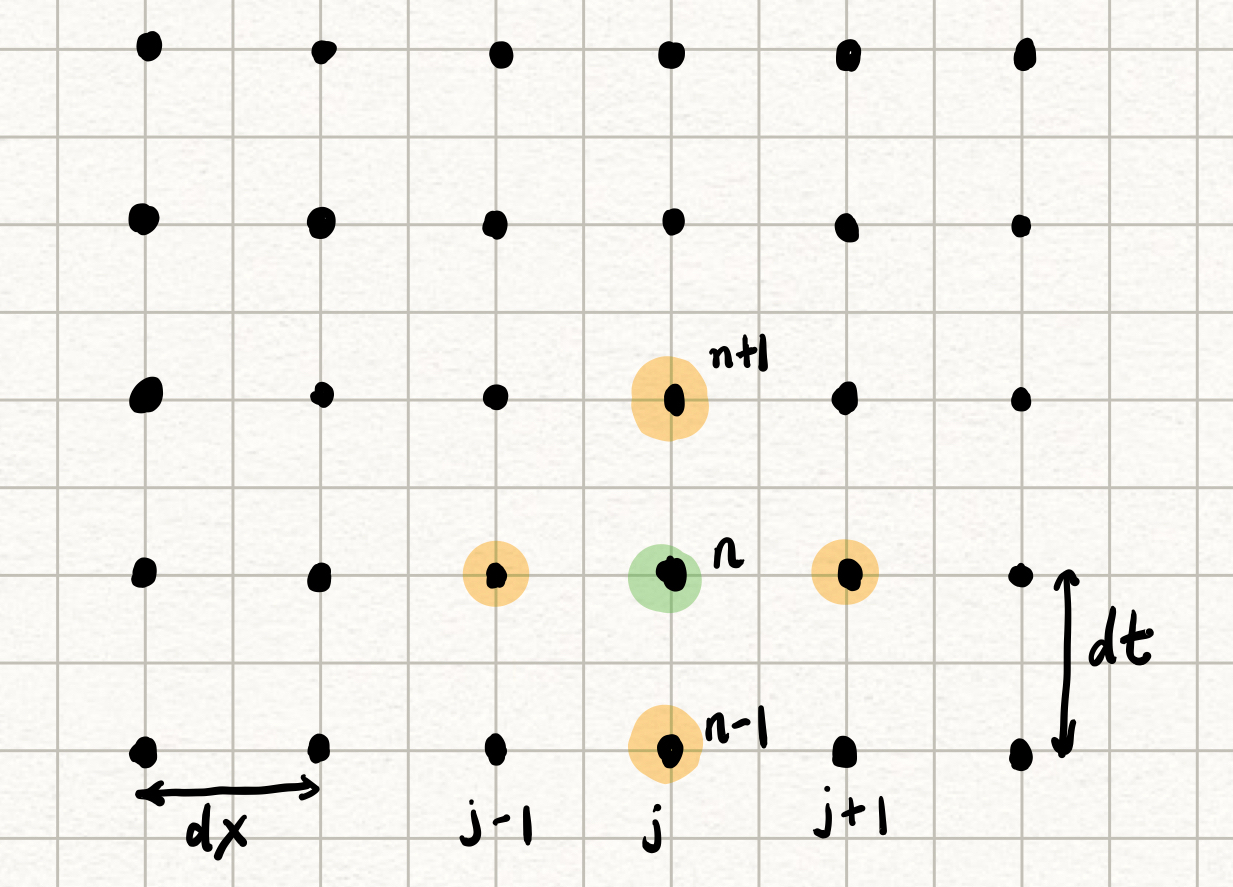
使用公式 $4$ , $5$ , $8$ , $9$ 中的差分算子代替波动方程 $1$ 中的微分算子，可以将波动方程近似为：

$\begin{matrix} (10) & \frac{u (x + Δ x, t) + u (x - Δ x, t) - 2 u (x, t)}{Δ x^{2}} = \frac{1}{c^{2}} \frac{u (x, t + Δ t) + u (x, t - Δ t) - 2 u (x, t)}{Δ t^{2}} + f (x, t) \end{matrix}$

接下来我们对连续的波动方程求解域离散化，对求解域进行均匀网格划分，空间和时间步长分别为 $Δ x$ , $Δ t$ , 如下图所示：

经过离散化的空间坐标和时间坐标可以表示为：

$x = x_{j} = j Δ x, j = 0, \pm 1, \pm 2, \dots$

$t = t_{n} = n Δ t, n = 0, \pm 1, \pm 2, \dots$

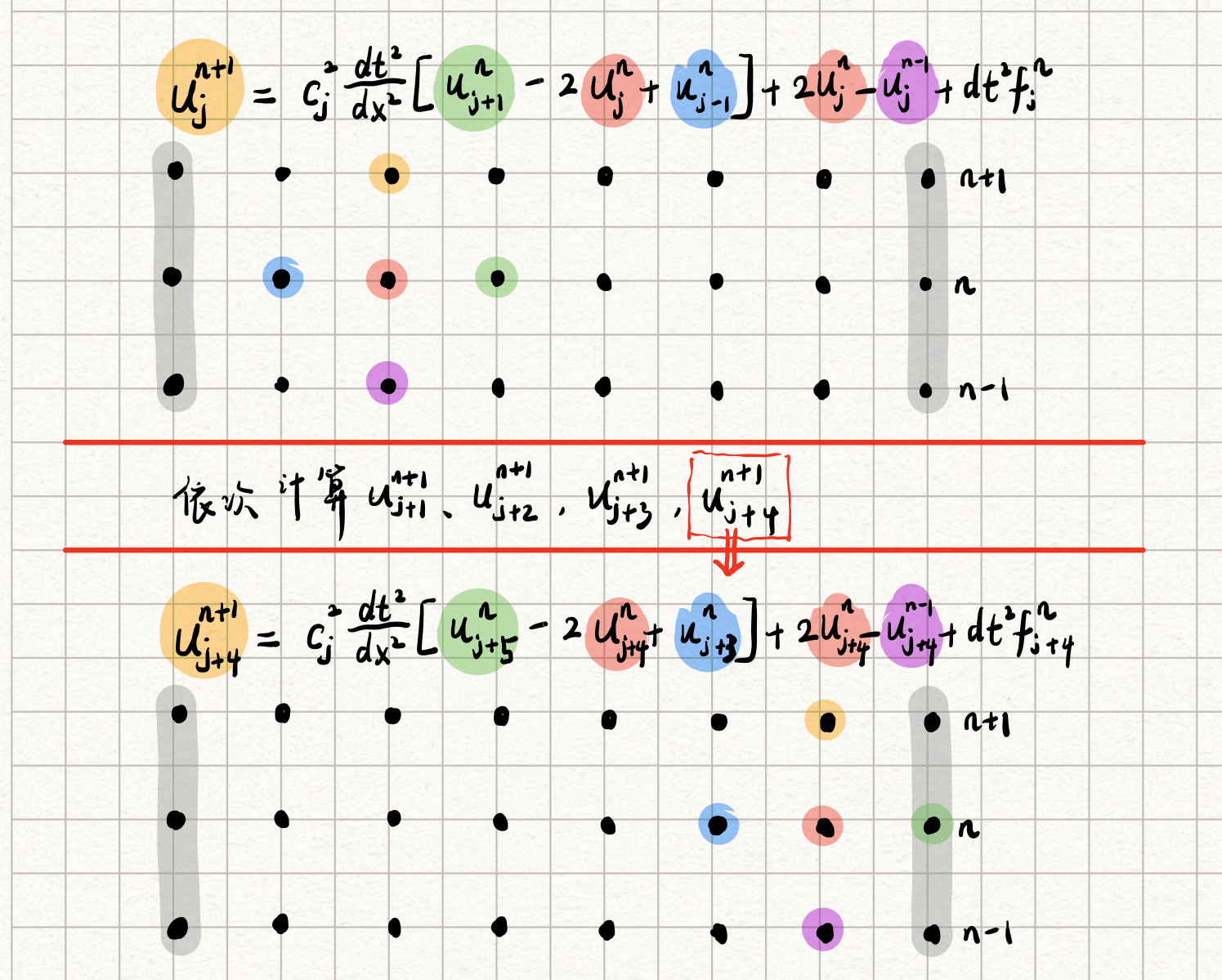
对求解域离散化后，可以将离散化的波动方程表示为如下式所示的形式：

\begin{matrix} (11) & \frac{u_{j + 1}^{n} + u_{j - 1}^{n} - 2 u_{j}^{n}}{Δ x^{2}} = \frac{1}{c^{2}} \frac{u_{j}^{n + 1} + u_{j}^{n - 1} - 2 u_{j}^{n}}{Δ t^{2}} + f_{j}^{n}, j = 0, \pm 1, \pm 2, \dots; n = 0, 1, 2, \dots \end{matrix}

将上式整理，得到 $u_{j}^{n + 1}$ 的外推格式：

\begin{matrix} (12) & u_{j}^{n + 1} = c_{j}^{2} \frac{d t^{2}}{d x^{2}} [u_{j + 1}^{n} - 2 u_{j}^{n} + u_{j - 1}^{n}] + 2 u_{j}^{n} - u_{j}^{n - 1} + d t^{2} f_{j}^{n} \end{matrix}

当第 $n - 1$ 层的值 $u_{j}^{n - 1}$ 和第 $n$ 层的值 $u_{j - 1} n$ , $u_{j} n$ , $u_{j + 1} n$ 的值已知时，可以直接计算得到第 $n + 1$ 层的值 $u_{j}^{n + 1}$ 。因此这种差分格式为三层显式差分格式。

在计算的过程中，先对计算同一时刻的空间离散网格上的 $u$ ，也就是先求每一层的值，上一层算完了再算下一层。下面这个图片可能对理解计算的过程有帮助。